学习知识的层次是：接触 → 理解 → 内化 → 应用 → 掌握。
人与人之间的区别主要产生在——“内化”环节。

连续与无穷

微积分 = 微分 + 积分

微分：把研究的对象分解成非常非常微小的单元去研究；（注意，每个微小单元要具备全局性质，“全息”）

积分：把刚才研究完的非常微小的单元，再积累在一起得到结果。

类似于“分析”与“综合”的关系。

英文 Calculus：“计算方法”

和我们常说的计算器——calculator 非常像，其实，它的原意就是“计算方法”的意思。

所以，最初，完整的微积分英文要这么说：

differential and integral calculus （“微分和积分的计算方法”）

另外也可以这么说：infinitesimal calculus （“研究无穷小量的计算方法”）

连续性：自然规律之大道

“连续”是研究微积分的重要前提。

在经典的物理世界中，一切都是连续的。

这里，我们假装不知道“量子世界”，只研究“连续函数”（Continuous function）——

连续函数一般表示为：\(f\left( x \right) \in C\)

无穷：是一个动态的概念

“无穷”是微积分的核心概念。

“一尺之棰，日取其半，万世不竭。”
—— 《庄子 · 天下》

右边的式子，“无限趋近”于 1。这是一个“动态过程”。

无穷小，是一个“变量”，是一个无限趋近于0的一个“过程”。

所谓“高阶无穷小”，无非就是它“趋近于0的‘速度’更快”呗。（此处有深意，与后面的洛必达法则有联系）

“无穷视角”看问题

例1 在一个无穷小的范围里，所有曲线都是直线：

例2 割圆术

“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣。”
—— 刘徽《九章算术注》（263年）

极限

极限是无限逼近的过程

这个过程的“终点”永远达不到，但是无比趋近的那个值，就是“极限值”。

比如，\(\lim_{x\rightarrow x_0} f\left( x \right) \) 表示变量 x 向 x₀ 点无限逼近，f(x) 无限趋近的那个值，就是极限值。

上文讲的无穷小本身是一个”过程”，这个过程的极限，就是0。

极限是一种线性运算

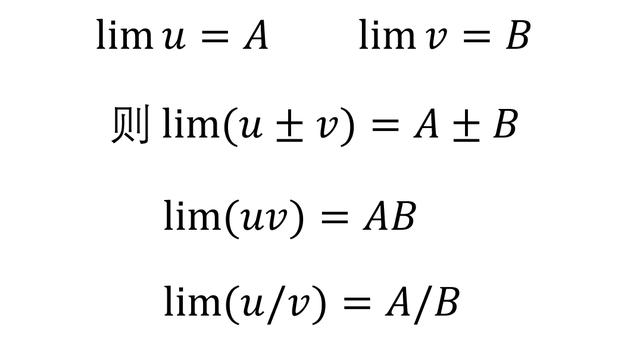
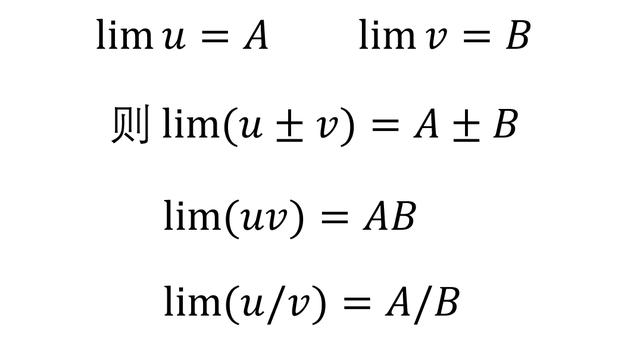
\(\infty /A=\infty \)

“吾生也有涯，而知也无涯。以有涯随无涯，殆已！”
——《庄子 · 养生主》

知识是无穷的，而生命却只有那么几天，所以算下来，想要学完所有知识，每天必须也学无穷多的知识，那还得了！

未定式极限的计算

指两种情况：\(0/0 \) 和 \(\infty / \infty \)

上文说，极限是一个过程，那么极限之间的比较，其实是在比较谁的速度快，这就是“洛必达法则”（求导后再比）。

或使用因式分解/化简——

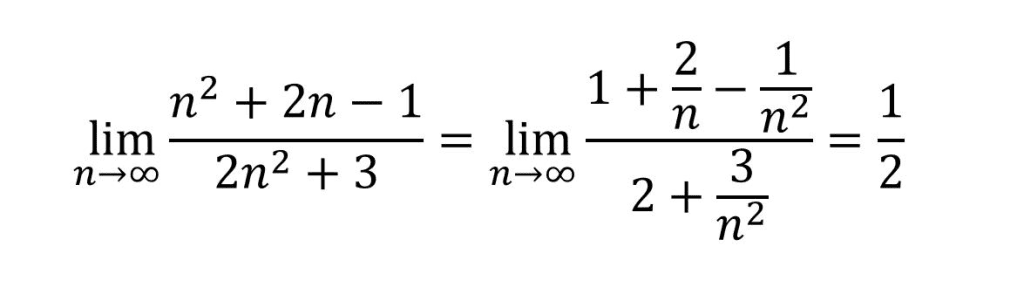
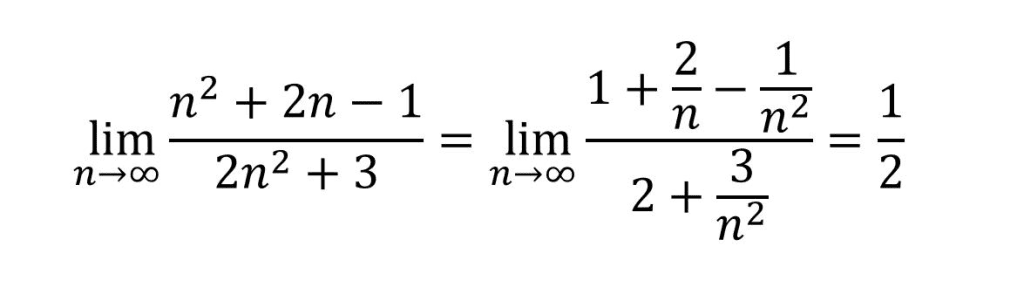
或替换变量或使用等价无穷小。

使用MATLAB计算极限

limit(fun,x,x0) % 求函数fun关于x在x0点处的极限
limit(fun,x,x0,'left') % 求左极限
limit(fun,x,x0,'right') % 求右极限

如果不是趋近于 x₀，而是趋近于无穷，就使用 inf 代表无穷，代替x0。

如果极限不存在，MATLAB会吐出一个“NaN”字。

limit 函数也能使用符号，比如——

syms x a b; % 把x a b都定义为符号
f=x*(1+a/x)^x*sin(b/x); % 输入函数
L=limit(f,x,inf) % 求极限

导数与微分

导数之“导”——導

组个词看一看：导致、引导、导向

“善战者，因其势而利导之。”
——《史记·孙子吴起列传》

“导”就是“方向”，导数就是表示函数“运行的方向”。

导数是“函数的原因”

“导数”是函数的原因（变化的来源），函数是“导数”的结果。

速度是位移的导数，速度导致了位移；加速度是速度的导数，加速度导致了速度。

用【导数思维】来分析问题，可以找到事物变化的原因，控制事物的发展。

“物有本末，事有终始，知所先后，则近道矣。“
——《大学》

理解乘法导数求导法则

\((uv)\prime=u\prime v+u v\prime\)

我们把 u、v 看成是一个矩形的边长，则 (uv)’ 就是指边长 u 和 v 同时变化，所引起的面积变化量。

矩形的面积变化量还有角落里的一小块，但是太小了，小到直接舍去。

导数的MATLAB求解

y=diff(fun,x) % 求函数 fun 关于 x 的导数

y=diff(fun,x,n) % 求函数 fun 关于 x 的 n 阶导数

微分：同样也是动态概念

微分就是差分的【无穷小过程】，自变量 x 的微分为：

\(\mathrm{d}x\,\,=\,\,\Delta x\left| _{\Delta x\rightarrow 0} \right. \)

这时，因变量 y 的微分为：

\(\mathrm{d}y=f’\left( x \right) \mathrm{·d}x\)

可以说，dy 是 Δy 的“线性主部”。

注意哈~ 不要觉得这里面有一个“误差”，这是“静态视角”下看到的，而微分是一个动态的无穷小过程，是完全没有误差的。

泰勒展开：多项式仿真系统

泰勒展开公式初探

\(f\left( x \right) =\sum_{n=0}^{\infty}{\frac{f^{\left( n \right)}\left( x_0 \right)}{n!}\left( x-x_0 \right) ^n}\)

观察后，发现有几个特点：

一个函数，无论它是什么“壳”，都可以分解为“多项式之和”的形式；
分解时，可以选择一个基础点 x₀；
项越多，就越接近原函数，无穷多项时取等号；
越靠前，越主要，每一项的作用，要被n!削弱。

比如正弦函数在 0 处分解——

\(\sin \left( x \right) =x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots \)

（偶数项的导数均为0，因此不在公式中）

用MATLAB画一下：

x=-6:0.01:6;
y3=x-x.^3/factorial(3);
y5=y3+x.^5/factorial(5);
y7=y5-x.^7/factorial(7);
plot(x,sin(x),x,y3,x,y5,x,y7)
ylim([-1.5 1.5])

只要项数 n 有限，就一定有误差，误差项为：

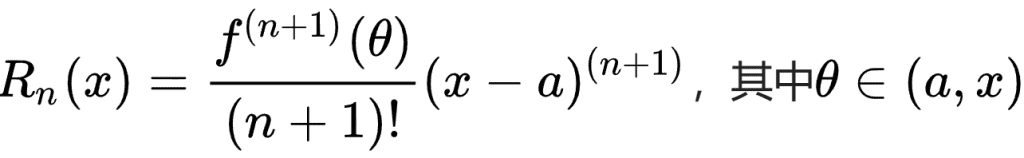
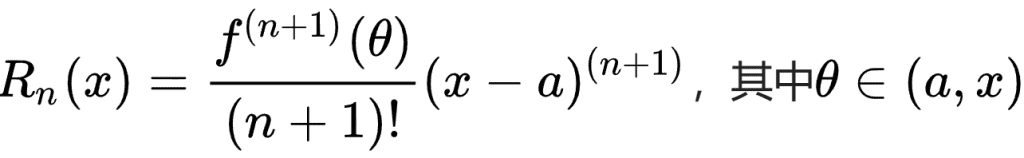
泰勒展开的哲学理解

先只展开前2项，解释为：x 处的函数值，约等于 x₀ 处的函数值，再加上由导数引起的变化量。

这是对未来情况的仿真。

几何表达：

由于原因（导数）只是“当前”的原因，所以仿真预测的结果肯定不完全准确；不过，只要时间足够短，仿真就足够准确。

二阶导数呢？就是原因的原因，即“间接原因”：

结果 ≈ 现状 + 直接原因引发的变化 + 原因的原因引发的变化+…

考虑得越多，就越准确、越长远。

“夫未战而庙算胜者，得算多也，未战而庙算不胜者，得算少也。多算胜，少算不胜，而况于无算乎!”
——《孙子兵法》

泰勒公式的提醒：本末/主次之分

公式直接展现了分析问题的步骤：

现状f (x₀) → 主因f ‘(x₀) → 次因f “(x₀)

预测的第一要务是要分清“本末”，现状为本，变化为末；引起变化的原因很多，也要先分“主次”。

“求之其本，经旬必得；求之其末，劳而无功。”
——《吕氏春秋》

积分为“果”：是“因”的降维投影

不定积分：求导的逆过程

函数 F (x) 的导函数为 F ‘(x) = f (x)，则：

f (x) 是 F (x) 的导函数；

F (x) 是 f (x) 的原函数。

注意哈，F (x) + C(常数) 的导数也是 f(x)，所以

f (x) 有一族原函数—— F(x) + C

表示为：

\(\left( F\left( x \right) +\mathrm{C} \right) ‘\,\,=\,\,f\left( x \right) \,\, \text{或} \int{f\left( x \right)}\mathrm{d}x\,\,=\,\,F\left( x \right) +\mathrm{C}\)

计算的话，有“换元积分法”和“分部积分法”等方法，MATLAB只需一句话：

F=int(fun,x) % 求函数fun关于x的不定积分

相同原因导致不同结果

一个导函数对应一簇原函数，这是因为，现状(C)不同。

这种关系类似于“投影”。

下面是一点个人理解：

低维世界的原函数是高维世界的导函数的投影。

原因在高维，结果在低维。

比如，小车的速度 v，相对于位移 s 是一个高维世界的信息，因为它：

决定了低维信息位移 s 的变化；
“不直观”，如果不投影低维的位移信息，我们甚至不易理解；
表达简单，“高维的表达反而简单”。

提示我们建立【升维思维】，可以解决许多实际问题。

定积分：有限范围内的求和

如何求一个曲线 f(x) 包围的面积？

分割无限小，再加起来，就是“定积分”。定积分求的是“曲线下面积”。

积分就是求和，积分号就是一个拉长的 S (sum)。

定积分：原因历经时间产生的作用

从定积分的基本定理就可见端倪：

定积分，是在计算“影响”：

定积分是“原因” f(x) 经过一段过程（从a到b）所造成的结果改变(影响)。

定积分的MATLAB求解

F=int(fun,x,a,b) % 求函数fun关于x的从a到b的不定积分

如果是无穷积分呢？

即a或b中至少一个是无穷量的积分，书本上称为广义积分或反常积分。

那就直接把a或b换成 inf，就OK。

傅里叶展开：频域下的谐波仿真系统

正弦波函数与余弦波函数，统一称为：谐波函数。

明明就是同一个函数，只不过“相位”不同而已。

谐，和也。
——《尔雅》

谐波：自然之道

世界由波组成：声波、光波、电磁波、地震波、应力波、引力波 …

而谐波是所有波中，最“和谐”的，它有一个重大的特性：

谐波的导函数还是谐波，谐波的原函数还是谐波！

比如，sin'(x) = cos(x) = sin(x+pi/2)，意思是，正弦的导函数还是正弦，只不过导函数要早了 π/2（1/4个周期）。

谐波：命运启迪

中国人在基因里已经刻入了对于谐波的理解，《易 · 乾》：

人在逆境中为什么能坚持住？就是因为他看到了命运的周期。

物极必反，否极泰来，反者道之动。

祸兮福之所倚福兮祸之所伏
——《道德经》

傅里叶分解：任意波都由谐波组成

“波”的本质即是“周期函数”，周期的倒数即为频率，任意一种波，是否能分解成不同频率的谐波的叠加呢？

\(f\left( x \right) =\sum_{n=0}^{\infty}{\left( a_n\cos nx+b_n\sin nx \right)}\)

\(a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos nx\mathrm{d}x}\quad b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \sin nx\mathrm{d}x}\)

傅里叶分解：频域上的谐波叠加仿真系统

比如，方波：

叠加项越多，越接近原始方波。

其实，这跟泰勒展开是一致的，越到后面的项，起作用就越小。

最右边那一列叫作：频谱

把时域的信息，变成频域信息了。图中表示了每一谐波项的频率（横轴）和幅值（纵轴）。

傅里叶展开，是通过不同频率谐波叠加的方式，对任意周期函数进行仿真的系统。

把波(振动)向频域分解后的应用

例1 比如一台机器，发生了不好的振动，那就把振动信号傅里叶分解出来，找到出问题的频率，然后再查哪个振动源是这个频率呀，就找到问题所在了。

例2 有限元可以计算零件的各阶模态的频率振型。

例3 一个低频信号，掺入了一些高频的噪音，那么可以采用傅里叶分解的方法，分解后直接将高频的部分舍去，这就叫低通滤波。

傅里叶展开的MATLAB源码

在MATLAB中，没有傅里叶展开的直接函数，但是我们可以依照公式写一个出来:

[A,B,F] = fseries(f,x,p,a,b) % 调用格式
% 以下为函数体
function [A,B,F] = fseries(f,x,p,a,b)
if nargin==3, a=-pi; b=pi; end
L=(b-a)/2;
if a+b, f=subs(f,x,x+L+a);end
A=int(f,x,-L,L)/L; B=[]; F=A/2;
for n=1:p
  an=int(f*cos(n*pi*x/L),x,-L,L)/L;
  bn=int(f*sin(n*pi*x/L),x,-L,L)/L;
  A=[A,an]; B=[B,bn];
  F=F+an*cos(n*pi*x/L)+bn*sin(n*pi*x/L);
end
if a+b, F=subs(F,x,x-L-a);end

两种仿真系统：泰勒与傅里叶

两者都是仿真系统，都是项数越多，误差越小，但是也有区别：

泰勒 分析运动的因果：着眼于从一点 x₀ 展开，离该点越远误差越大，用多项式揭示运动的量化规律；

傅里叶 分析频率的构成：着眼于全局周期性，从频域的角度找到原函数的高维特征。

微分方程就是因果关系

微分方程（Differential equation，DE）表示的是原函数(果)与导函数(因)之间的关系。

比如，y‘ = 1，就是最简单的微分方程了。是一阶微分方程（最高阶导数的阶数）。

解是：y = x + C

如果再加一个条件（初始条件）：y(0) = 0

这样，解就只能是 y = x 了。

微分方程：现代科学的基石

大致上可以这么说，一个学科是不是科学，就是看有没有微分方程。

因为，研究一个量的导数的规律，才有可能从根本上理解这个量的规律。

微分方程，展示的就是原函数(果)与导函数(因)之间的关系。

微分方程解析解

事实上，微分方程不太好解，教材上一般也就列举了几种很特殊的微分方程的解法，但其实真到了使用微分方程的时候，往往不在这几种列举的范围之内。

“君子生非异也，善假于物也”
——《劝学》

MATLAB求解微分方程，一般用 dsolve 函数就能搞定。

例1：

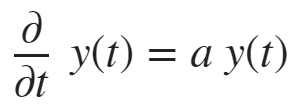
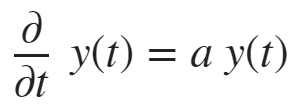
syms y(t) a % 符号
eqn = diff(y,t) == a*y % 函数
cond = y(0) == 5; % 条件
ySol(t) = dsolve(eqn,cond) % 解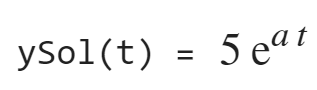

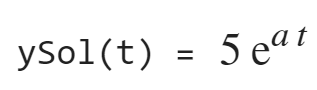
例2：

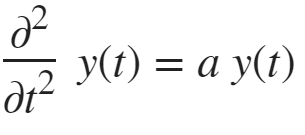
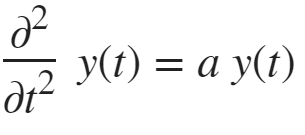
syms y(t) a 
eqn = diff(y,t,2) == a*y
ySol(t) = dsolve(eqn)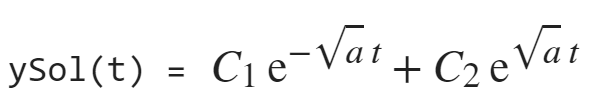

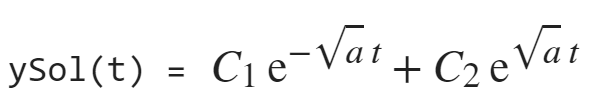
微分方程数值解

其实，许多微分方程根本求不出解析解，只能求出数值解。

啥叫数值解？

就是说，虽然求不出函数的表达式，但是我能知道函数在各处的值，这个值不是绝对准确，但是在一定的精度范围内。

MATLAB中最常用的解常微分方程(ODE)的函数为 ode45（四阶五级变步长算法）——

例，解方程：y ‘ = 2t

tspan = [0 5]; % 求解范围
y0 = 0; % 初值条件
[t,y] = ode45(@(t,y) 2*t, tspan, y0); % 方程以函数句柄形式来定义
plot(t,y,'-o')

没有表达式，只有由点组成的“数值解”。

如果非得写成表达式的形式，也好办，拟合回去呗。

微分方程造就了有限元法

大名鼎鼎的“有限元法”（FEM，Finite Element Method），其实只是一种求解微分方程的数值解法。

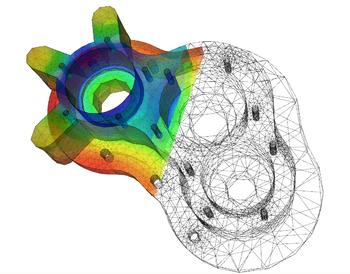
所谓“仿真”，就是对模型的计算。FEM的元模型，就是微分方程，也就是事物之间的因果关系。

思想总结

“无穷”是微积分的基础核心。

“导数”是函数的原因，函数是“导数”的结果。

泰勒展开：多项式仿真系统，提醒我们本末/主次之分。

傅里叶展开：频域下的谐波仿真系统，提醒我们在频域中寻找本质特征。

微分方程就是因果关系，是现代科学的基础核心，也造就了有限元法。

“你最好学学微积分，它是上帝的语言。”
—— 费曼

极简内化微积分：核心概念与思想